На 17 април в пощата на Математически анали, един от най-добрите журнали в сферата, пристига документ. Написан от математик почти непознат на експертите в полето – 50 и нещо годишен лектор от университета на Ню Хемпшир на име Итанг Джанг – документът претендирал за постигането на голям напредък в разбирането на един от най-старите проблеми в математиката – хипотезата за прости числа близнаци.
Редакторите на изтъкнати математически журнали са свикнали с получаването на грандиозни твърдения от неизвестни автори, но тази претенция се различавала от останалите. Написана с кристална яснота и пълно разбиране на проблема и неговото настоящо състояние, изследването се доказвало като сериозно и редакторите на Аналите решили да му дадат бърз старт.
Само три седмици по-късно – период, който може да бъде приет като едно премигване, в сравнение с обичайното темпо на развитие при математическите журнали – Джанг получил доклада на рецензента си.
„Основните резултати са първокласни”, пишел един от рецензентите. Авторът е доказал „важна теорема за разпределението на простите числа.”
Слуховете, че никому неизвестен изслеовател – някой, чийто талант бил толкова подценяван, че след получаването на докторантурата му през 1992 му било трудно да си намери академична работа; някой, който работил няколко години като счетоводител и дори в магазин на „Събуей” – успял да направи такъв голям пробив, бързо и проправили път сред математическата общност.
„На практика никой не го познава” – казва Андрю Гранвил, теоретик на числата от Университетът на Монреал. „Сега, изведнъж, той показва едни от най-големите резултати в историята на теорията на числата.”
Математици от Харвард набързо уредили Джанг с презентация пред претъпкана аудитория на 13 май. С разкриването на детайли от работата на Джанг, става ясно, че той постига резултатите си не чрез радикално нов подход към проблема, а чрез прилагането на вече съществуващи методи с голямо постоянство.
„Големите експерти в областта вече са опитвали да приложат този подход,” казва Гранвил. „Той не е познат експерт, но успя там, където всички експерти се провалиха.”
Проблемът на двойките
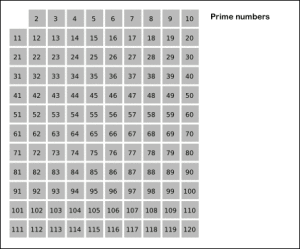
Простите числа – тези, които нямат други делители освен 1 и себе си – са атомите на аритметиката и са пленявали математиците още от времето на Евклид, който доказал преди повече от 2 000 години, че има безкрайно много прости числа.
Тъй като простите числа са фундаментално свързани с умножението, разбирането на техните събирателни свойства може да бъде подвеждащо. Някои от най-старите нерешени проблеми в математиката се отнасят до базисни въпроси за простите числа и събирането. Такива например са хипотезата за простите числа близнаци, според която има безброй много двойки прости числа, които имат разлика 2, и хипотезата на Голдбах, според която всяко четно число е сбор от две прости. (По невероятна случайност, по-слаба версия на втория въпрос е разгледана в изследване, публикувано он-лайн от Хералд Хелфгот от École Normale Supérieure в Париж, докато Джанг изнася лекцията си в Харвард.) (http://arxiv.org/pdf/1305.2897v1.pdf)
Простите числа са в изобилие в началото на числовата редица, но стават все по редки сред по-големи числа. От първте 10 числа, например, 40% са прости – 2, 3, 5 и 7. Сред 10-цифрените числа обаче, само около 4% са прости. Повече от век математиците знаят как простите числа намаляват средно аритметично: сред големи числа, предполагаемото разстояние между две прости числа е приблизително 2.3 пъти повече от броя на цифите. Така например, сред 100-цифрените числа, предполагаемото разстояние между две прости числа ще бъде около 230.
Това обаче е само средно аритметично. Простите числа често са по-близо едно до друго, отколкото средно аритметичното предполага, или пък са на по-голямо разстояние. В частност, простите числа „близнаци” често се появяват случайно – двойки като 3 и 5 или 11 и 13, които имат разлика само от 2. Въпреки, че подобни двойки стават все по-редки сред големите числа, простите числа близнаци никога не изчезват напълно (най-голямата такава двойка, открита до момента, е 3,756,801,695,685 x 2666,669 – 1 и 3,756,801,695,685 x 2666,669 + 1).
Стотици години математиците размишляват върху съществуването на безкраен брой двойки прости числа близнаци. През 1849 година френският математик Алфонс дьо Полиняк разширява тази хипотеза до идеята, че трябва да съществуват безброй много прости двойки за всеки възможен краен период, не само за 2.
Оттогава насам присъщата привлекателност на тези хипотези ги е превърнала в математическия свещен граал, нищо че до момента тяхно приложение не е известно. Въпреки много положени усилия за доказване на тези хипотези, математиците не са били способни да отхвърлят възможността, че периодите между простите числа нарастват и нарастват, като в крайна сметка прехвърлят всякаква специфична обвързаност.
Днес Джанг чупи тази бариера. Неговото изследване показва, че съшествува число N, по-малко от 70 милиона, такова че съшествуват безброй много двойки прости числа, разликата между които е N. Независимо колко навътре в пустините на наистина огромните прости числа навлезете, независимо колко редки тези числа стават, винаги ще намирате прости числа, които се различават помежду си с по-малко от 70 милиона.
Резултатът е „поразителен”, казва Даниъл Голдстън, теоретик на числата в щатския университет на Сан Хосе. „Това е една от онези задачи, за които не си сигурен дали някога някой ще може да реши.”
Просто сито
Семената, чийто резултат Джанг жъне могат да бъдат намерени в изследване от преди 8 години (http://arxiv.org/abs/math/0508185), което теоретиците на числа наричат GPY, кръстено на трите си автора – Голдстън (Goldston), Янош Пинтз от Института по математика „Алфред Рений” в Будапеща (János Pintz) и Джем Йълдъръм от Босфорския университет в Истанбул (Cem Yıldırım). Това изследванестига изкусително близо до резултатите на Джанг, но се оказва крайно неспособно да докаже съществуването на безброй много двойки прости числа с някакъв краен период между тях.
Вместо това, то показва, че винаги ще има двойки прости числа, които ще са много по-близки едно до друго, отколкото средно аритметичното разстояние предполага. По-точно, GPY показва, че за всяка избрана фракция, независимо колко малка е тя, винаги ще има двойка прости числа, които ще са по-близки от фракцията на средно аритметичния период, ако се продължи достатъчно дълго по линията на числата. Изследователите обаче не могли да докажат, че периодите между тези прости числа винаги ще са по-малки от някое определено крайно число.
GPY използва метод, наречен „пресяване”, за филтриране на двойки прости числа, които са по-близки от средно аритметичното предположение. Ситата дълго са използвани в изучаването на простите числа, започвайки от Ситото на Ератостен (използва се и Решето на Ератостен) от преди 2 000 години – техника за намиране на прости числа.
За да използваме Ситото на Ератостен за намирането на всички прости числа, да кажем до 100, трябва да започнем от 2 и да зачеркнем всички по-големи числа, които се делят на 2. След това преминаваме на 3 и да зачеркваме всички числа, делими на три. Тъй като 4 вече е зачеркнато, преминаваме на 5 и зачеркваме всички числа, които се делят на 5, и така нататък. Числата, които оцелеят след зачеркването, са простите числа.
Ситото на Ератостен работи перфектно за намирането на прости числа, но е твърде тромаво и неефикасно, за да бъде използвано за решаване на теоретични въпроси. През последния век теоретиците на числа развиват колекция от методи, които осигуряват полезни приблизителни отговори на такива въпроси.
„Ситото на Ератостен върши твърде добра работа,” казва Голдстън. „Модерните методи, които използват сита се отказват от перфектното пресяване.”
GPY развива сито, което филтрира списъци с числа, в които е напълно възможно да има двойки прости числа. За да се стигне до реалните прости числа, изследователите комбинират ситото с функция, чиято ефективност се основава на параметъра „степен на разпределение”. Този параметър изчислява колко бързо простите числа започват да показват определени закономерности.
Степента на разпределяне е определена на поне 1/2. Това е точната степен, която позволява резултатите на GPY, но тя не е достатъчна за доказването на съществуването на двойки прости числа в определен интервал. Ситото на GPY може да установи такъв резултат, но само ако степента на разпределение на простите числа може да се докаже като повече от ½. Всяко по-гоямо количество би било достатъчно. Според изследователите това поставя теоремата на GPY на косъм желаните резултати.
Колкото повече обаче изследователите се опитват да преодолеят това препятствие, толкова по-дебел става косъма.
През късните 80 години на миналия век трима изследователи: Енрико Бомбиери – носител на медала на Фийлдс в Института за напредничави изследвания в „Принстън”; Джон Фрийдландър от университета в Торонто и Хенрик Иваниец от университета „Рутгърс”; развиват начин за откъсване на определението на степента на разпределение, за да увеличат стойността на този коригиран параметър до 4/7. След разпространението на изследването GPY през 2005, изследователите започват да работят трескаво за включването на тази променена степен на разпределени в пресяващата рамка на GPY, но без успех.
„Големите експерти в областта се опитаха и се провалиха,” казва Гранвил. „Лично аз не вярвах, че някой ще успее в близкото бъдеще.”
Затваряне на периода
През това време Джанг работи в уединение, опитвайки се да преодолее пропастта между резултатите на GPY и хипотезата за ограничените периоди на простите числа. Той е китайски имигрант, който завършва докторантура в университета Пърдю. Винаги се е интересувал от теорията на числата, макар и тя да не е тема на дисертацията му. През трудните години, в които не успява да намери академична работна позиция, той продължава да следи развитията в полето.
„Има много възможности в една кариера, но най-важното е да продължиш да мислиш,” казва той. Джанг прочита изследването GPY и обръща специално внимание на изречението за близостта „на косъм” между GPY и ограничените интервали между простите числа. „Това изречение ме впечатли много,” казва той.
Без да се свърже с експертите в областта, Джанг започва да мисли върху проблема. Три години по-късно, най-сетне успява да постигне някакъв напредък. „Бях толкова изморен,” казва той.
За да си почине, Джанг посещава приятел в Колорадо през лятото. Там на 3 юли, по време на кратка дрямка, преди да отиде на концерт, той открива решението. „Веднага разбрах, че ще проработи,” казва той.
Идеята на Джанг е да използва не ситото от GPY, а негова модифицирана вресия, в която ситото филтрира не през всяко число, а само през числа, които нямат големи прости делители.
„Неговото сито не върши толкова добра работа, защото не се използва всичко, с което можеш да пресяваш,” казва Голдстън. „Оказва се обаче, че, въпреки че е малко по-неефективно, то позволява гъвкавостта, която позволява на решението да работи.”
Според Голдстън, това ново сито позволява на Джанг да докаже, че има безброй много двойки прости числа, които са по-близо едно до друго от 70 милиона, но едва ли може да бъде приложено в хипотезата за простите числа близнаци. Дори с най-силните възможни предположения за стойността на степента на разпространение, казва Голдстън, най-добрите възможни резултати от метода GPY ще бъдат, че има безброй много двойки прости числа, които имат разлика от 16 или по-малко помежду си.
Гранвил обаче казва, че математиците не трябва преждевременно да отхвърлят възможността за достигане до хипотезата за простите числа близнаци по тези методи.
„В тази работа играта се променя и понянога след ново доказателство, това, което преди е изглеждало изключително трудно, се оказва просто малко разширение,” казва той. „Това, което трябва да направим сега, е да разучим изслеването и да видим кое какво е.”
Гранвил казва, че на Джанг са му били необходими няколко месеца, за да обработи детайлите, но резултатът е модел за ясно изложение. „Той заковава всеки детайл, така че никой не може да се усъмни в него. Няма ненужен пълнеж.”
След получаването на оценката на рецензента, събитията около Джанг се развиват с бясна скорост. Поканите за представяне на работата му започват да преливат. „Мисля, че хората са развълнувани от факта, че някой изведнъж постигна това,” казва Гранвил.
За Джанг, който се счита за срамежлив, блясъка на прожекторите е някак неудобен. „Казах си, „Защо така изведнъж?”, казва той. „Беше толкова объркващо, понякога.”
Все пак Джанг не е толкова срамежлив по време на представянето си в Харвард, което присъстващите възхваляват за неговата яснота. „Когато изнасям лекция и се концентрирам върху математиката, забравям своята срамежливост”, казва той.
Джанг не изпитва никакво огорчение относно доскорошната си неизвестност и несполуките в кариерата си. „Умът ми е много миролюбив. Не се интересувам много от парите или честта,” казва той. „Харесва ми да съм тих и да работя сам.”
Същевременно Джанг вече работи по нов проект, който отказва да опише. „Надявам се, че ще има добър резултат,” казва той.