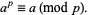Превел: Тихомир Георгиев
Увод
Просто число е такова естествено число, което се дели само на единица и на себе си. Следователно тези числа не могат да бъдат разложени. Първите 10 прости числа са 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29. Числото 1 не е просто число, въпреки че е било считано за такова в миналото. Причината за това не е нещо загадъчно, а просто за да се направи валидна основната теорема на аритметиката.
Създаването на метод за откриване на прости числа е математическо приключение, продължаващо векове наред – от древните египтяни до днес. Все още предстои да бъде намерен точен модел в лабиринта от числа, въпреки че е имало многобройни опити.
Свойствата на простите числа се изследват задълбочено теорията на числата – клон на математиката фокусиран върху естествените числа.
История
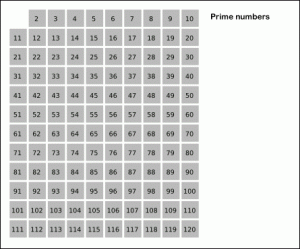
Доказано е, че простите числа за пръв път са изучавани задълбочено от древните гърци (например Евклид). Гъркът Ератостен е създал метод за намиране на всички прости числа по-малки от дадено положително число. Неговият изненадващо ефикасен метод е много добър старт за по-нататъшното развитие на теорията на числата. При своя метод (Решето на Ератостен) той започва като написва всички числа от 2 до зададеното число. След това той зачерква всички числа, делящи се на 2, след това тези делящи се на 3 и така нататък докато зачеркне всички възможни числа. Няма да му отнеме време да зачерква числата делящи се на 4, защото те се делят и на 2. С други думи той зачерква само числата делящи се на тези прости числа, които не са по-големи от квадратен корен от числото посочено като горна граница на търсенето. Например за да намери простите числа по-малки от 100 той би зачеркнал само тези, които се делят на прости числа по-малки от 10 (квадратен корен от 100). Тогава незачеркнатите числа са прости числа.
Решето на Ератостен
Свойства
- Няма най-голямо просто число. Това може лесно да се докаже чрез довеждане на обратното предположение до противоречие. Ако имаме поредица от последователни прости числа P = [p(1), p(2), p(3)… p(L)] където p(1) е първото просто число, p(2) е второто просто число…, а p(L) е предполагаемото „най-голямо“ просто число, тогава кое число е делител на числото p(1)*p(2)*…*p(L) 1? Интересно е, че числото трябва да е просто, но различно от p(1) … p(L), което е невъзможно.
- Има безкрайно много прости числа (това е перефразиране на горното свойство). Ойлер доказва, че сумата от обратно пропорционалните на простите числа е безкрайна: 1/2 1/3 1/5 1/7 1/11 … = ∞
- Всяко естествено число по-голямо от 1 може да бъде представено по уникален начин като произведение на поредица от едно или повече ненамаляващи прости числа. Това свойство се нарича основна теорема на аритметиката.
- Ако
е просто число и
е естествено число, тогава
Освен това, ако
не е делител на
, тогава съществува
такова, че
е 1 mod
. При умножаване на горното по
се получава:
- Според положителния отговор на Чебишев на въпроса на Бертран, ако n е положително цяло число, по-голямо от 1, тогава винаги има просто число pn < p < 2n. така че
- Най-голямо просто число познато досега е 232,582,657 − 1.
- Простите числа се основните компоненти в криптографските RSA алгоритми.
Има и много други свойства…
Специални прости числа и нерешени задачи
- Мерсен се интересувал от простите числа от типа 2 n – 1. Когато такова число е просто, то и n е просто. Такива числа 2 n – 1 се наричат прости числа на Мерсен. Те са се появили още в Евклидовата теорема за „перфектните числа“ повече от хиляда години преди раждането на Мерсен. Най-големите познати прости числа са Мерсенови, но засега все още не знаем дали Мерсеновите прости числа са безкрайно много. Мерсеновите числа 2 p – 1 не е задължително да са прости, когато p е такова; например 211 – 1 = 2047 което се дели на 23 и 89.
- Ферма въвежда числата наречени на негово име. Те са F(n) = 2 2 n 1 за всяко не отрицателно цяло число. Ферма погрешно е считал, че всички тези числа са прости. Днес се знае, че безкрайно много от тях са съставни, но не се знае дали и простите са безкраен брой. Тези числа на Ферма F(n), за които се знае че са прости са само за n = 0 … 4. За няколко от числата на Ферма е доказано, че са съставни.
- Двойките прости числа (p , p 2) наричани прости числа близнаци се срещат доста често при сравнително малките прости числа, например {3 5}, {5 7}, {11 13}, {17 19}, {29 31}, {41 43}, {59 61} и т.н. Като цяло Виго Брун показва, че тези двойки не са толкова чести, като доказва, че сумата от технните обратно пропорционални числа е крайна за разлика от тази на обратно пропорционалните на всички прости числа (споменатата по-горе теорема на Ойлер. Ние все още не знаем дали тези двойки прости числа са безкрайно много.
- Хипотезата на Голдбах (в строгата формулировка а Ойлер) твърди, че всяко четно цяло число по-голямо от 2 може да бъде представено като сума от две прости числа (например 4 = 2 2, 6 = 3 3, 8 = 5 3, 10 = 7 3 = 5 5, 12 = 7 5 и т.н.). Тази проста и недвусмислена хипотеза все още не е доказана.
- Хипотезата на Риман за зета-функцията е за нулите на функция с комплексна променлива, наречена зета-функция. Тази хипотеза на Риман може да се интерпретира като твърдение за „прости вълни“. Когато отчетете всички тези вълни и ги сумирате за да направите една функция, получавате функция, която напълно описва поведението на простите числа. Такъв важен феномен все още не е доказан.
- Има и много други нерешени задачи:
- Безкрайно много ли са тези прости числа p за който p 2 и p 6 също са прости?
- Безкрайно много ли са тези прости числа p за който p 4 and p 6 също са прости?
- Безкрайно много ли са тези прости числа p за който 2⋅p 1 също е просто? Те се наричат прости числа на Софи Жермен.
- Безкрайно много ли са простите числа от вида x2 1? Този въпрос е зададен от Едмънд Ландау.
Всички тези въпроси (включително зададения по-рано въпрос за двойките прости числа) и почти всеки въпрос, който можем да си представим са частни случаи на прочутата хипотеза на Шинзел.
Източник: http://knol.google.com/k/prime-numbers